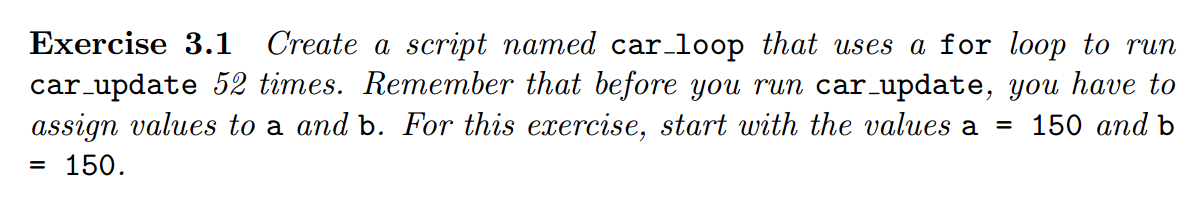Final Project: Completion and Reflection

Our project is complete!  We finished the construction and attaching everything together, made sure the code works correctly, and tested the sound levels.  Here are several pictures of our final prototype.

Front

Back

Arduino (in middle) and two protoboards (on each side)

Servo motor and actuator for "Good Job" message

Servo motor and actuator for "Too Loud" message
and battery pack (black box on left) connected to Arduino

Video of final project in action

This project challenged us in every way possible, but the fact that we created something from scratch that actually works makes me very proud.  It was great to see all we had learned this semester was being put to use as we created this device.  If we had more time, Sabrina and I would like to continue working on the code to make the transitions even smoother and to work more on our potentiometer so the teacher is able to change the settings.  We would also like to clean up the wiring on the back, and find a way to hide the wires on the back and on the sides.

Sabrina (left) and I with our final project

Final Project: Construction and Coding

After we completed our design and figured out materials last week, we started the construction of our device.  We had to wait for our LEDs and transistors to arrive, so in the meantime we wrote our code using three single LEDs and tested them with our sound sensor and Servo motors.

This was the first code we wrote that made the LEDs turn on and off correctly according to the sound level.  We used three red LEDs and labeled them Red, Yellow, and Green.  To test the sound level, we used a tone generator and also tried using our own voices.

Next, we figured out the Servo motors.  We can set the Servos to a position from 0 to 180.  The following code, we have the commands for the motors in each if-else statement.  The "Too Loud" message shows when the red section is on, and the "Good Job" message shows when the green section is on.  For the yellow section, there is no message.  Below is our code with the Servo motors.

Once we had our LED strips arrived, we began soldering each row together.  The red section has 5 rows of 4 strips, the yellow section has 5 rows of 3 strips, and the green section has 5 rows of 2 strips.  The soldering was one of the most time-consuming parts of our project.

We then connected the LED to the Arduino to make sure they worked.  Some of the soldering wasn't perfect, so the yellow section had some trouble with the colors.  We have our 4 LED strips, 2 Servo motors, and the sound sensor connected to the Arduino.  It is powered by a 9V battery pack that is connected to the protoboard through the Vin pin.

We then incorporated the LED Strips into the code.  The LED strips use code that is a little bit different from the single LEDs.  Each strip has a red, green, and blue wire.  For the red section, we use only the red.  For the yellow section, we use red and green to create yellow.  And for the green section, we just use the green wire.  So in our code and on our Arduino, we are using four pins in total for the LED strips.  The main difference is that the yellow uses two pins, and we turn both of them on to create yellow.

Once the code, LEDs, and Servos worked, we used the laser cutter to print out the back piece, the two messages, and the 3 smiley faces.  The LED strips have adhesive on the back, so we attached all of the LEDs to the Delrin back piece.

The next step for us was attaching everything on the back of the Delrin:  the two servo motors and actuators, the two protoboards, the battery pack, and the Arduino.   For the two Servo motors with messages, we used Legos to create a track for the actuator and we built small platforms for the motors with gears.  We used hot glue to secure the Legos and motors.  The two protoboards have adhesive on the back, so we put them on either side of the Arduino.  The Arduino is held by building Legos around it, so that it is easily removable.

Finally, we wanted to make the transition between each section less jerky and so we averaged the readings from the sound sensor over time.  We tried two different approaches to this problem, and found that the following code worked the best.

Final Project Design Changes and Materials

Last time, we ended with our foam model of the "wave" shape with LEDs set in curved rows to match the top of the design.  As we began looking into our materials, such as LEDs, we realized that we did not want to solder together a million individual LEDs.  So, we headed over to Adafruit to look for strips of LEDs that can be red, yellow, and green.  We found these RGB LED Strips.  However, these LEDs we will be using can't bend, so we must arrange the LEDs in straight rows instead of curved.  We did some thinking on the board about how to arrange these and how many we needed.  

In this picture, we were thinking of 10 rows of LEDs for each section, but later we spaced them out so we only use 5 rows.  We still wanted the red section to be the largest, so that the sound level is related to the size of the section, so the strips in the red section would be longer than in the green section.  Here are our final calculations for the LEDs.   We decided we needed 4.5 meters of LEDs, but we can't order a half meter, so we ordered 5 meters.

The picture above is our guide for construction of our project.  It shows the spacing of the strips, and how many we need for each section.  The LED strips are 10 cm long, but they come connected together.  Each row will be already connected, but then we will have to solder each row in a section together.

Next, we needed to make sure we have everything to use these LEDs.  Adafruit has a great resource on using and wiring these LEDs: RGB LED Strips Usage.  These LEDs require transistors, and Adafruit recommends using a N-channel MOSFET STP16NF06.  Each strip (in this case each section because the strips will be soldered together for each individual section) usually requires 3 transistors, one each for the red, green, and blue wires.  

So in theory we would need 9 transistors; however, for the red section, we only need 1 for the red wire because we won't be using green and blue.  And for the green section, we only need 1 for the green wire because we won't be using the red and blue.  To create yellow, we only need red and green, so we will need 2 transistors.  So in total we ordered 4 transistors.

Those were the only materials we needed to buy online.  Our other materials we have in the engineering lab.  These are:

-Arduino Uno

-Protoboard

-Lego NXT Sound Sensor

-Servo Motors

-Lego Gears

-Lego Actuator

-Delrin (for backing piece, faces, and messages)

-Solder and wires

-Legos (to attach sound sensor and motors)

-Tools/Hot Glue/Laser Cutter

Arduino Day 5 (Line Following)

Our last task with the sciborgs is to create a sciborg that follows a white line on the ground.  This task with the sciborg took the longest, so Olivia and I worked on some of it outside of class because we are also learning MATLAB and doing final projects in class.

Brightness Sensor

To create a line-following sciborg, we used a LEGO brightness sensor.  The line that the sciborg will follow is a line of white tape on a brown board.  The sensor reads values of brightness, so the white line was around values of 540 or less and the brown board was values of around 570 or more, and the values are printed in the serial monitor.  The following is the basic code for the brightness sensor.

The values are printed in the serial monitor, so before we started on the next task, we played around with the light sensor and a test piece of the track to get some base values for the white strip and the brown background.  We decided to have the brightness sensor calibrate on the white tape.  So we would set the sciborg down with the brightness sensor on the white tape, then plug the batteries in, and it would calibrate to the white tape.

Line Following using Bang-Bang Control

For the bang-bang control we decided to have 3 different levels.  It took us a long time to figure out the different levels and how it would turn both left and right.  If the brightness is less than 540, it goes straight.  If it is greater than 574, it turns right.  And if it is between those two values, 540 and 574, it turns left. This works because as the light sensor moves away from the white line, the values continue to get larger.  We arrived at these numbers through lots of testing, which was probably the longest part of this project.

This is a diagram of what we wanted the sciborg does within the three different ranges. It is supposed to go straight when it senses the white line, but if it goes off the line on the right side, it turns left to get back to the line.  If if goes off on the left side, we have already set a range on each side that makes it turn left, but then that left turn pushes it into the next range, which makes it turn right.

Here is our final code for bang-bang control.  We use the values in our if-else statements.  Inside each statement, we have the code for each movement that corresponds to the range.  In the last else statement, we have the car turning left and then moving forward a tiny bit.  This helps the sciborg on the left side of the line.  When it reaches the first range, it will turn left, and go straight a tiny bit, which helps it reach the "turn right" range, and it will get back to the line.

As I said previously, too get the sciborg to follow the line as best as possible, we had to do a lot of testing.  We changed the values and speeds many times before we finally got a combination that worked very well.  Some of the troubles we had were when the sciborg went to the right of the line, it would start turning left, but wouldn't make it back to the line in time, so it would start turning right (because the second "turn right" range is on both sides).  Here are a few videos of our sciborg following the line.

Line-Following using Proportional Control

After Olivia and I finished our bang-bang control for the line-following, we moved on to proportional control.  Proportional control in this case means that the further away from the line that the sciborg is, the faster the speed of the turn.  For the turning speed, we multiply 60 by the difference in brightness value.  The difference in the brightness value depends on the range values.  For the left turn, we subtract 540 and for the right turn, we subtract 570.  This tells how far away from the line the sciborg is, and so the farther away from the line, the faster the turn speed.

Final Project Brainstorming and Design

Brainstorming

My partner, Sabrina, and I did some brainstorming for our final project.  We spent about 15 minutes just coming up with many ideas and then narrowed it down to two general projects: Hand Washing and Noise Level.  We presented our ideas for these two projects in class.

Sabrina and I decided on the project on the left that helps children control their noise level in the classroom.  We took some of our basic ideas and brainstormed more about specific design details, such as the mechanisms, how we would connect lights and motors, and what would happen for each sound level.  

When we went over our ideas and narrowed it down, we came up with this first idea:

-Three colored areas of the circle.  Each third of the circle would have LEDs on the outside rim corresponding with the color of the section, and there would be the corresponding face in the middle of each section.

-A Servo motor in the center (behind the circle) controls an arrow that moves between the areas

- The lights turn on one by one as the arrow moves around the circle.  For example, as the arrow passes a light in the green section, it turns on, and then the next one as the arrow passes it, etc.  When the volume lowers again, the arrow moves backward, and each light turns off as the arrow passes it

-Motor also controls messages next to colored areas.   The messages correspond to each color and noise level.

-The sound sensor attached near bottom, connects to the Arduino on the back.

Design

Initial Design Ideas

We started out with this original circular design with three colored wedges, similar to the one in the image above.  Our design later changed to be a linear representation rather than a circular representation.  This is because young children understand the linear progression more than the circular idea.

Keeping this in mind, we changed our second main idea to a shape like volume symbol of a computer, a shape that fanned out like a sound wave.  We got rid of the arrow that pointed to each section and set up the LEDs in curved rows.  We kept the smiley faces and the messages.  We created a rough foam model of this design

Questions to consider

As we made our model and talked about design, we came up with lots of questions.  We went back and talked to one of the teachers in the classroom.  The following are some questions and notes we took down that addressed some questions and issues.

Are flashing LEDs too distracting for the kids?

Yes, flashing LEDs would make the students too interested in it.  Our LEDs will just light up and not flash.

What sound volume is too loud and too soft?

There are different appropriate sound levels during, for example, nap time and play time.  Sabrina and I will go to their classroom and do testing on the sound sensor.  We will possibly have different settings for the teacher to adjust during different activities, using a potentiometer that adjusts the parameters for each color.

Where is a good place for this and how should it be powered?

We visited the classroom and found a good spot on the wall in the oldest classroom.  The teacher said battery-powered would be the best, so that the device can be portable, and could be used in many different places.

What should the messages be for the different red/yellow/green sections?

The messages can be just on the red and green sections.  We are going to create messages that are easily detachable and changeable so that the wording can be changed.  The messages will be behind the device and will be moved out by an actuator, gear, and Legos. 

MATLAB Introduction

MATLAB

We started our new unit today on MATLAB.  I am working with my new partner Sabrina on this unit (Here's her blog: sabrinaattemptsengineering.blogspot.com)  We will also be working on the final project together.

We started by reading the first four chapters of Allen Downey's Physical Modeling in MATLAB and doing some of the exercises to familiarize ourselves with programming in MATLAB.


Exercise 2.1 -  Fibonacci Sequence 

The fibonacci numbers are a sequence of numbers where the next number is the sum of the previous two: 1, 1, 2, 3, 5, 8, 13, 21, . . .   The following is our first exercise to learn simple coding in MATLAB, and to make sure we got the order of operations correct.

In our code, we decided to split the expression inside the brackets into two elements.  By doing it this way, we reduce the number of parentheses we must use and we don't get so confused.  We name these elements by creating variables called first_element and second_element, and then use those variables in the next expression.  In the command window below, you can see that when we set n = 10, the answer is 55, which is the 10th term in the Fibonacci sequence.

Exercise 2.3 - Car Rental Update

Now things got a little more complicated.  We had the following problem to solve and code.  Our first step was actually understanding the problem and the math behind it.  We did some diagrams and created equations to work it out.

At first, we had our equations as you see in the following code.  To update the number of cars for a, we take away 5% of a and add 3% of b.  The equations are correct, but we realized we were missing a step when the numbers did not come out correctly. The problem is the following:  a and b both start at 150.  Then a updates.  Then b updates, but when b is updating, it is using the value for a that has already been updated, not the original 150.  We fixed this problem in the second code below.  We update the values using anew and bnew and then set a and b to the new values.  After several weeks we see that the number of cars reaches an equilibrium.

Car Update (Almost Correct!)

Car Update (Correct!)

Exercise 3.1 - Car Update with Loop

For the next exercise, we kept the same problem and the same code, but just added a for loop to the code.

Here, we take our code from the last example and add a for loop.  Inside the loop, we have our previous function that updates the number of cars.  The loop runs 52 times, so that the last values will show the number of cars in each location at the end of 52 weeks (1 year).

So at the end of a year, we see that the number of cars in each location reach an equilibrium.  To visualize this, we will learn in the next exercise that we can plot these points over time.



Exercise 3.2 - Car Update Loop with Plot 

Next in our reading we learned how to make plots from our code.  We took our previous code for the Car Update Loop and added code to plot the points.  This way we could see the equilibrium that each city reached.

We added three lines to our code.  "Hold on" tells the plot to keep the previous points during the loop.  Then we plot the values of a versus i with 'ro' red circles.  Then we plot the values of b versus i with 'bd' blue diamonds.

Y-axis: Number of cars.  X-axis: Time in number of weeks.
Initial number of cars in Albany and Boston is 150.
Albany (a) is represented by red circles and Boston (b) is represented by blue diamonds. 

Exercise 3.5 - Fibonacci Sequence with Loop

Now, back to the Fibonacci sequence.  This time, we will add a loop that can compute any number in the sequence.  

First, we have to tell it the first two terms: 1 and 1.  Here we are using a function notation, where F is the function and the number in the parentheses is the term number.  Hence F(1) means the first term and F(2) is the second term.  So F(n) means that we can set n to be something and compute the nth term.  The for loop will run from 3 to n, and inside the loop all we have is the function specifying the Fibonacci sequence.  The next term is the sum of the previous two terms.

To test our code, we set n to be 10, and the result was 55, which is correct.  We tested out 15 and the 15th term of the Fibonacci is 610!

Exercise 4.6 - Fibonacci Ratios with Plot

This last exercise was the most confusing of the afternoon.  It took us a while to actually understand the question.  Basically, take the Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, . . .  and divide the next term by the previous term, so 1/1 = 1;  2/1 = 2;   3/2 = 1.5;  5/3 = 1.667.  These are the ratios we want to compare.   Over time these ratios converge, or get close to one number.  If I list out the ratios, you can see that they start to converge somewhere around 1.618:  1,  2,  1.5,  1.667,  1.600,  1.625,  1.615,  1.619,  1.618,  1.618.  You can see these ratios in the command window below.

In our code, we have the loop from last time and the only thing we added was the second for loop/  For this loop we have it going from 2 to n, and the function we have is R(n) for ratios.  It take the nth term and divides is by the n-1 term.  For example if I were computing R(2), it would be R(2) = F(2)/F(1), which is 1/1 and so R(2) = 1.  Then, we plot ratio versus n with blue circles.

In the following plot of the Fibonacci ratios, we can see the convergence behavior.  For the first 10 or so terms, the ratios are drastically different and after that, the ratios only differ by small decimals so they seem to converge on one value.

Final Thoughts

That is it for our first day of MATLAB!  I found coding in MATLAB to be pretty similar to the other coding languages I already know, just a few minor syntax differences.  It was great to see that we can apply this to useful situations and I can see why MATLAB is used to model so many things in the sciences.  Next class, we will using MATLAB to model thermal systems, heating and cooling things down.  Also, since we were given our partner assignments today, we will be working on our project during the next few classes in addition to finishing up MATLAB, so look for those updates as well!

Final Project Ideas (CSC Visit)

For our ENGR 160 final project, we are going to design products to improve young childrens' classroom experiences.  We observed preschool-aged children during their class time and talked to the teachers about some of the problems they had in the classroom.  We asked them what we might be able to do to help them in the classroom and what could help the children.

Some challenges we learned about were:

• Keeping the children on their mats:
• During certain class times, the teacher has all the children sit on small rectangular mats to keep them still. Sometimes the kids stray off their mats, and teachers have to constantly remind them to stay on their mats.

• Letting them know not to splash water out of the water table:
• Each classroom has a water table with toys in it for children to play with.  However, they often like to splash water around and it gets on the floor, making it slippery.

• Making sure the noise level is not too loud
• The classrooms often get loud during free play time, especially with older children.  Teachers must frequently remind them to use their inside voices.

• Reminding the kids to wash their hands with soap and water after using the bathroom

• The kids are sometimes scared by the toilet flushing loudly

• The lock on the bathroom isn't easy to open.

A few ideas I am interested in are monitoring the noise level in the class, keeping the kids on their mats, and making sure the kids wash their hands after the bathroom.

Noise Level ideas

• Creating some type of meter with red, yellow, and green
• Using something that senses noise level or loudness
• Need to make sure it doesn't make sound or excite children too much

Keeping Children on Mats

• Touch sensor on mat
• Light turns on when child is not on mat, turns off when child is on mat
• Maybe have a tool for the teacher to know who is off their mat

Washing Hands

• Sound of toilet flushes causes something to happen at sink, maybe a light or message reminder
• Lights indicating steps of hand washing
• Ultrasonic sensor to sense when child is at sink

Arduino Day 4 (Sciborg Part 2)

Today, we learned about and experimented with three new feedback mechanisms: motor encoders, touch switch sensor, and ultrasonic sensor.  Then, we will use these sensors with our sciborg to implement two types of control: bang-bang control and proportional control.

Motor Encoders

The following sample code for encoders measure the number of rotations of the motors.  The encoder reads the current position and these values are printed.  In the sample code, the wheel moves backward and forward, and the encoder reads the current position of the motor.  The starting value for the encoder should be zero because we reset the encoder to zero in the void setup when we have "m.set_pos(0)".  The end value is not zero because we don't reset the encoder to zero within the loop.

Touch Switch

There is a touch switch on the front of our sciborg.  This can detect when the touch switch is activated and when it is not (e.g. the sciborg runs into an obstacle).  The touch switch is wired to a digital pin on the Arduino and also to ground.

Wiring for Touch Switch and LED

The following sample code includes the LED and the touch switch. When the touch switch is pressed, the LED turns on, but stays on forever and will not turn off when we let go of the touch switch.  Our job was to fix this and make the LED change according to the touch switch. We wanted to modify the sample code to make the LED turn on when the touch switch is pressed down and turn off when the touch switch is not pressed down.  All we have to do is add an else statement to the if statement.

Touch Switch with LED

At first, the LED did the opposite of what we wanted.  It would turn off when the switch was activated and stay on when it was not activated.  We weren't really sure what was happening, but played around with the code and wiring to see what was going on.  The code below is what we had for our first attempt.

Then, we modified the code once we figured out what was wrong.  The code in the loop is identical from the previous picture, but we think it had to do with the mode of the touch switch in the setup.  The mode in the first attempt was just "Input" (we're not sure what happened there?) and in the following code for the second attempt, we changed the mode to back to "Input-Pullup".  This switches the input. Additionally, for some reason it would not work when we wired the touch sensor to the LED, so as you can see in the comments, we took that wire out from our first attempt.  In the video, we have the LED turning on and off with the touch switch.

Ultrasonic Sensor

The ultrasonic sensor measures the distance from objects surrounding around it.  For example, if nothing is in front of the sensor, the printed values are large, and then as the sensor approaches a wall, the values become smaller, indicating there is something close to the sensor.  As you might guess, this can be useful for helping our sciborg avoid obstacles.  The following is the sample code for the ultrasonic sensor.  The sample code here gives value in the serial monitor that corresponds to distances.  A low number indicates something is near to the sensor and a large number indicates the sensor does not sense anything near it.  The sensor can also pick up readings from the sides, not just straight in front of it.

Feedback and Control

A. Fixed Distance, bang-bang control

In Day 3 of Arduinos we made our sciborg travel 10 feet by determining the time it would take and setting out motors to stop after that given amount of time.  In this bang-bang control task, we were able to get our sciborg within a few centimeters of 10 feet.

**Explain testing of values

Now we are using our new sensors to have the sciborg stop in different ways.  We used the ultrasonic sensor to control the point at which our sciborg would stop in front of an obstacle.  In our testing, we found that using the ultrasonic sensor, our sciborg would stop about 10cm short.  We could lower the parameter of how far away it should stop, but the ultrasonic sensor also isn't very steady.  A very lower value doesn't the sciborg to stop in time.

This code is a combination of the ultrasonic sensor code and basic motor sciborg code.  We have the ultrasonic sensor reading values and the motors are controlled by those values.  If the sensor does not sense anything in front, meaning the sensor values are greater than 30, the motors are set to forward at full speed and if the sensor senses an obstacle, meaning the values are less than 30, the motors set the speed to zero.

B. Fixed distance, proportional control

First we had our sciborg travel 10 feet using bang-bang control, and now we want to use proportional control.  Proportional control means that, as the sciborg gets closer to its goal, its speed will be proportional to the remaining distance.  Thus, it slows down as it gets closer to 10 feet.

Using proportional control means we need to do some calculations.  Here in our code the equation we used was Speed = distance * gain, where distance is the distance remaining or error (goal - actual) and gain is a constant that we calculate.  We find the gain constant by taking the maximum speed of the motors 255 and dividing by the total distance.  In this case, we are using the distance 13000 because that is the number of rotations (measured by the encoder) needed to travel 10 feet.  We determined this value by testing different encoder values for the sciborg.  Our gain constant is 0.0196.  Our encoders count down from 13000 to 0, so we take the current reading from the encoder and multiply this by the gain constant. So when the sciborg is at the beginning, it's position is 13000 and this multiplied by 0.0196 is the maximum speed 255.  (This is because we divided 13000 by 255 to get the gain constant in the first place).  Then as the sciborg continues, the current encoder value is decreasing and multiplying by the gain results in a smaller number for the speed.  Therefore it slows down.

There is a typo in this code.  In the last if statement the gain constant should be 0.0196, not 0.02125.  Originally we had a higher gain constant, but later re-did our calculations.  The sciborg in the video is running the correct code.

You might notice there is a function in our code called nudge().  In proportional control, one issue is that around 9 feet, the speed has been getting smaller and smaller, so the sciborg is moving very slow and at some point can no longer move.  However, it hasn't reached 10 feet.  As we found earlier, the sciborg has a minimum speed where the motors are no longer able to move the car.  This value is around 50 for our sciborg.  To solve the problem, we created a function that nudges the sciborg to the end when it can no longer move under the proportional control.  If the speed of the sciborg gets lower than 70 and the sciborg has still not reached its goal, we call a function called  nudge.  This function turns the motors on and off and will continue to do so until 10 feet is reached.

C. Conga Line

Next implemented bang-bang control and proportional control in a different task.  This is the conga line, where we want the sciborg to follow something in front of it.

For bang-bang control, we decided to have the sciborg turn left or right.  Here, if the sensor doesn't sense anything the car turns left and if it senses something it turns right.  This way, when we moved our sheet of Delrin in front of it, it moves forward and slightly right, and then when we moved back with the Delrin it moved forward and slightly left.  This allows our sciborg to 'search' for objects in front of it to follow, while also (somewhat) traveling in a straight line.

At first, we didn't think about doing bang-bang by just having the sciborg move forward.  We could do this by having he motors turn on when nothing is in front of the sensor (meaning the Delrin is further in front of it)  and turn off when something is in front of the sensor (when it's really close to the Delrin).

When we coded for the the conga line with proportional control, we had our sciborg just traveling straight.  Proportional control for the conga line involves having the sciborg move faster when the Delrin sheet is far away and slower when the Delrin sheet is close.

Our next step is using bang-bang and proportional control to have our sciborg follow a white line on the floor.  We are going to use a new sensor that measures brightness!

Arduino Day 3 (Sciborg Part 1)

On Day 3, we started building and programming sciborgs, which are small cars run by 6-AA battery packs.  We attached the battery pack, the Arduino, and the protoboard to the sciborg, and then put a cover on top of the Ardunio that allows us to attach motors and sensors.



SOS Example

We used this example to learn about functions in Arduino.  In this example, there are two functions that are later used in the loop.  Using functions saves time and code writing.

Single Motor

Then, we attached the motors to the Arduino and ran the example program Single Motor. This program runs only one motor and results in the wheel moving backward and forward. We took this program as a starting point and modified it to create our next programs.

Double Motor

This program runs both motors at the same time and speed, so that the wheels of the sciborg move together and it will travel in a (hopefully straight) line.  We modified the original Single Motor program by adding the second motor and setting its speeds exactly the same as the first motor.

Minimum Speed

Next, we tested out different speeds on the sciborg.  We determined the lowest possible speed that made our sciborg still move was around 50.

Here is our sciborg moving incredibly slow!

Hard Turn

Now that we had our sciborg moving in a straight line, we had to figure out how to turn it.  First, we made the sciborg do a hard turn, essentially spinning it around in place.  To do this, we have each motor running at the same speed in opposite directions.

Gentle Turns

Since we don't want it to turn so abruptly, we needed to find how to implement some more gentle turns.  First, we had the sciborg go forward, turn a little, go forward, turn a little, and repeat.  This was successful, but resulted in a somewhat jerky turn.

The next gentle turn we tried out was smoother than the first.  One motor was set slightly faster than the other.  The result was the at the sciborg turned in a small circle.

10 feet

Next, we programmed our sciborg to travel exactly 10 feet.  We initially did this using the delay, finding just the right amount of time for the vehicle to move 10 feet.  After this determined time, which we found to be 9 seconds, we stopped the motor.  In our testing, the sciborg traveled the 10 feet exactly almost every time.  If it was off, it usually was short of 10 ft by about 2-3 cm.

Motor Button

After creating and testing some basic programs, Olivia and I started work on our biggest task of the day: when the sciborg hits an obstacles it backs up, turns, and continues on its way.

First, we needed learn how the Lego motor button worked, so we ran the example program Motor Button on our sciborg.  When the button is pressed, the motors stop, and when it is released, the motors start again.  In the following video, the motors have been set to opposite speeds, so the sciborg turns one way direction, then when the button is pressed and let go of, it turns the other direction.

Hitting a Wall

Now that we had played around with the motor button, we started on the code for hitting the wall.  This code makes the sciborg move straight, then when the button is pushed (it hits the "wall"), the sciborg backs up and turns.  Then the loop restarts and the sciborg continues straight until it hits something else.  For testing, we attached the motor button to the front of the sciborg.